
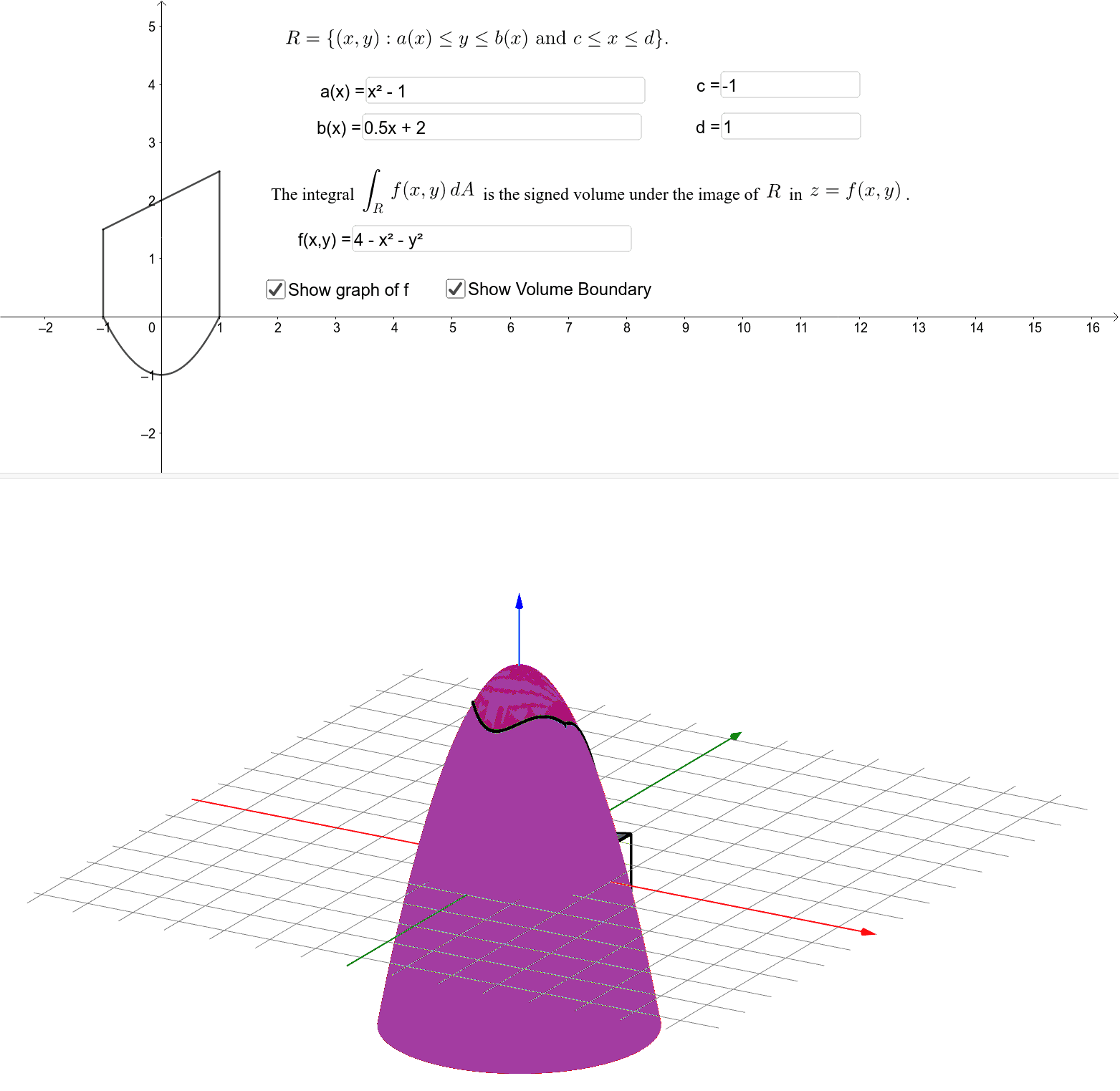
What is the benefit of such a calculation? The integral can be reused in another physics interface, which may be influenced by the accumulated energy in the system.
INTEGRAL GEOMETRY CALCULATOR HOW TO
How to use an additional physics interface for temporal integration. The source term of this domain ODE is the integrand, as shown in the following figure. The integral can be calculated as an additional dependent variable with a Distributed ODE, which is a subnode of the Domain ODEs and DAEs interface. The variable for the total heat flux is automatically calculated by COMSOL and is named ht.tfluxMag. Suppose, for example, that at each time step, the model requests the time integral from start until now over the total heat flux magnitude, which measures the accumulated energy. Similar to the Coefficient Form PDE example shown above, this can be done by adding an ODE interface of the Mathematics branch. If temporal integrals have to be available in the model, you need to define them as additional dependent variables. Temporal Integration by Means of Additional Physics Interfaces Similar operators are available for integration on spherical objects, namely ballint, circint, diskint, and sphint. How to use the built-in time integration operator timeavg. The following surface plot shows the resulting integral, which is a spatial function in (x,y): Of course, our users can also use integration in COMSOL for their own means, and here you will learn how. Integration also plays a key role in postprocessing, as COMSOL provides many derived values based on integration, like electric energy, flow rate, or total heat flux. A couple of examples of these are Total heat flux or floating potential. Having a closer look at the COMSOL simulation software, you may realize that many boundary conditions are formulated in terms of integrals.
INTEGRAL GEOMETRY CALCULATOR SOFTWARE
This blog post gives an overview of the integration methods available in the COMSOL software and shows you how you can use them.ĬOMSOL uses the finite element method, which transforms the governing PDE into an integral equation - the weak form, in other words. Once a PDE needs to be solved numerically, integration most often plays an important role, too. Partial Differential Equations (PDEs) are usually derived from integral balance equations, for example. Because spherical shells are uniformly dense, we assume that the center of mass is (0,0,0) and therefore all three integrals are zero.Integration is one of the most important mathematical tools, especially for numerical simulations. A 3-dimensional object’s volume is calculated by using the triple integral.īased on the definition of center of mass, your integrals represent the product of mass and its x, y, and z coordinates, respectively. The volume integral is a particular case of the triple integral.
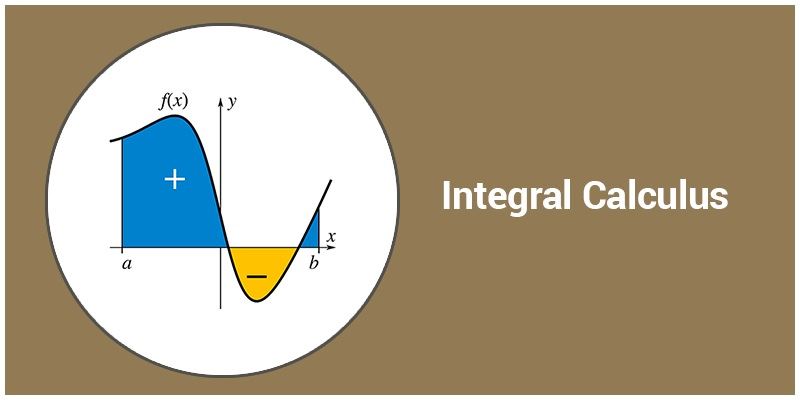
As a rule, integrals are used to measure the area under a curve, whether open or bounded. What is the relation between triple integrals and volume? The double integral is used for integrating over a two-dimensional region, while the triple integral is used for integrating over a three-dimensional region.

What is the difference between double and triple integral? We can use them to compute the volume under a surface, among other things. $$\int_ f(x) dx$$ is the signed area underneath the curve when your integrand is a function.ĭouble integrals are a way of integrating over a two-dimensional area.


 0 kommentar(er)
0 kommentar(er)
